Chapter 8 Lotteries

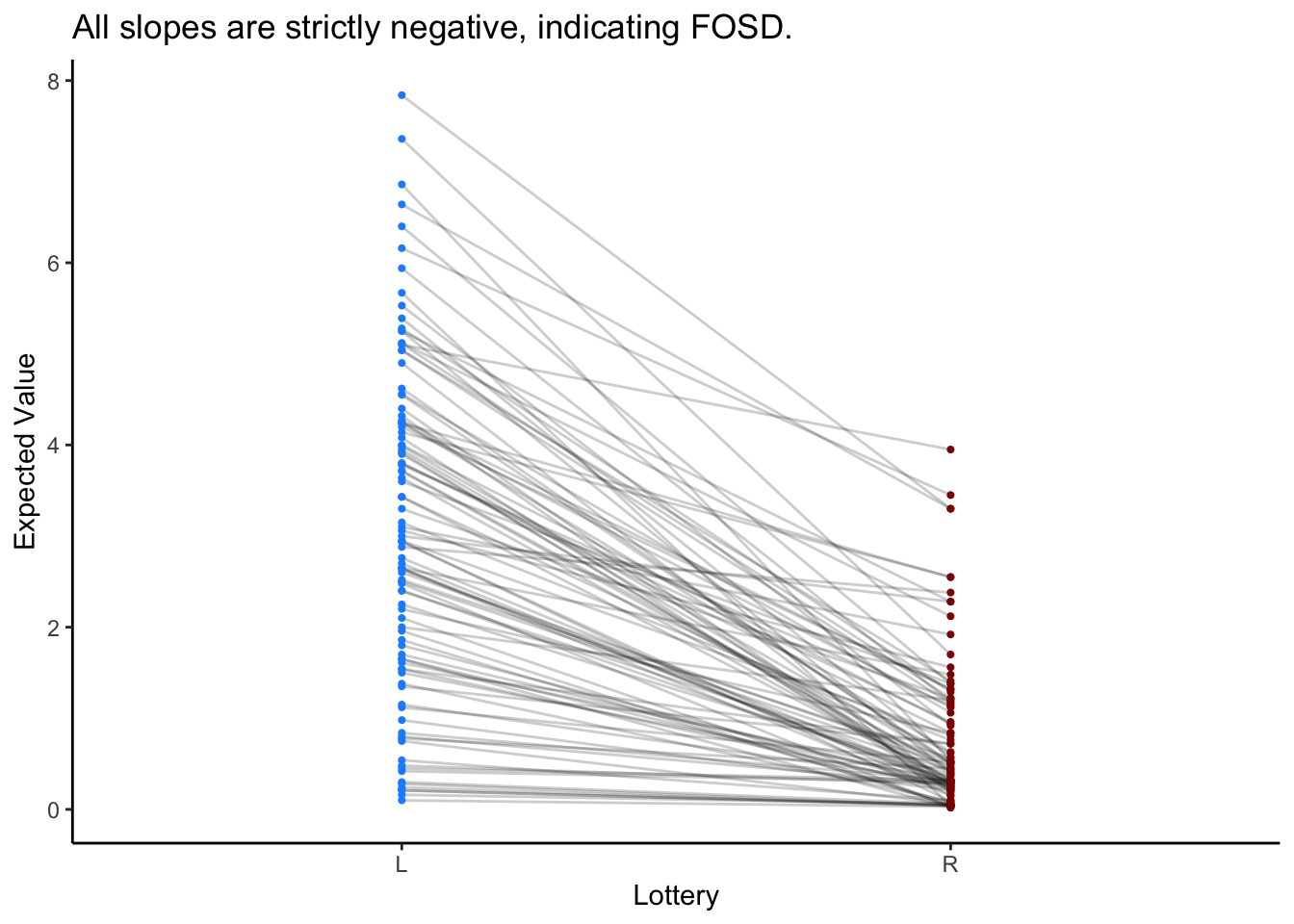
Generate vectors of lotteries. Lottery L will FOSD Lottery R.

L_prb = sample(c(2:99), 100, replace=T)/100
L_amt = sample(c(5:8), 100, replace=T)
R_prb = rep(NA, 100)
R_amt = rep(NA, 100)
for (i in 1:100) {
  R_prb[i] = sample(c(1:(L_prb[i]*100-1)), 1, replace=T)/100
  R_amt[i] = sample(c(1:(L_amt[i]-1)), 1, replace=T)
}

8.1 Expected Value

There are different ways to compare the lotteries. (Not Recommended) Since the DDM is a sequential sampling model, the order in which information (attribute values) enter into the decision process matters (Yang and Krajbich 2023, Fisher 2021). That being said, this would require eye-tracking and a whole bunch of other assumptions, so it may not be the simple explanation you’re looking for. (Recommended) You can just compare the expected values of the lotteries (Eum et al. 2024).

pdata = data.frame(L_lottery = "L", L_ev = L_prb*L_amt, R_lottery = "R", R_ev = R_prb*R_amt)

ggplot(pdata) +
  geom_segment(aes(x = L_lottery, xend = R_lottery, y = L_ev, yend = R_ev), color = "black", size = .5, alpha = .2) +
  geom_point(aes(x = L_lottery, y = L_ev), color = "dodgerblue", size=.75) +
  geom_point(aes(x = R_lottery, y = R_ev), color = "darkred", size=.75) +
  theme_classic() +
  labs(y = "Expected Value", x = "Lottery", title = "All slopes are strictly negative, indicating FOSD.")